다익스트라 알고리즘은 IT 개발자로 종사하는 사람이라면 모르는 사람이 없을 정도로 유명하면서도 기본적인 알고리즘이다.
이 알고리즘은 교통망이나 통신망과 같이 그래프로 나타내어질 수 있는 자료 구조에서 최단거리를 구할 수 있는 방법을 제시한다. 정확히는 한점으로부터 목적지까지의 최단경로트리를 만듦으로써 최단거리를 구한다.
다익스트라 알고리즘은 다음 아이디어에서 기반한다.
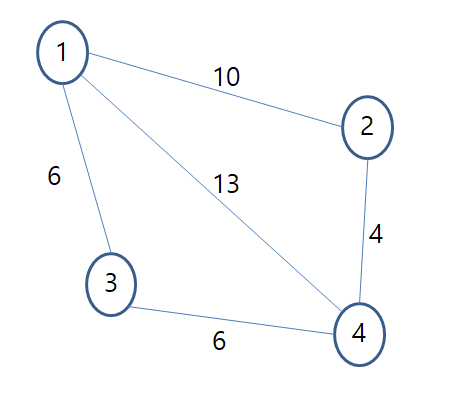
위와 같은 그림이 있고 간선 위의 숫자가 거리를 나타낸다고 하자.
위의 그림에서 1->4 까지 가는 최단 경로는 어떻게 직관적으로 계산할 수 있을까?
우리는 직관적으로 1->4 로 직접 향하는 1->4 경로의 비용(13) 보다 1->2->4 로 가는 경로의 비용(14) 이 더 크고, 1->3->4 로 가는 경로의 비용(12) 이 최적이라는 것을 알 수 있다.
우리가 직관적으로 파악할 수 있는 이 내용은, 바로 각 노드들까지의 경로는 "각경로의 최단거리의 합 중 가장 작은값" 이라는 걸 알 수 있다.
즉, A-B-C 로 연결된 리스트가 있을 때, A-C 로 가는 최단 경로는 반드시 A-B와 B-C 의 최단경로를 지나치게 된다는 점이다.
다익스트라 알고리즘은 이를 이용해서 최단경로를 저장하는 배열을 만들고, 노드들간의 최단경로를 계속해서 업데이트해주면서 최종적으로 출발지(src) 에서 목적지(dest) 까지의 최단경로를 만들어낸다.
다익스트라 알고리즘은 구현에 따라 Naive 하게 접근하는 방법과 Priority Queue 를 이용해 개선한 방법이 있다.
Naive 한 알고리즘은 노드의 갯수 N에 대하여 O(N^2) 만큼의 시간 복잡도를 가지며 다음과 같다.
/**
* 다익스트라 알고리즘.
* @param dist 최단경로 배열
* @param n 노드의 갯수
* @param src 시작 노드 인덱스
* @param dest 도착 노드 인덱스
* @return
*/
private static int djikstra(int[][] dist, int n, int src, int dest) {
int[] checkers = new int[n+1];
int checkCount = 0;
checkers[src] = 1;
checkCount++;
while (checkCount < n) {
int minIdx = -1;
int minDist = INF;
//새로 갱신된 최단경로를 dist 배열에서 새로 읽어온다.
for(int i=1; i<=n; i++) {
if(checkers[i] == 0 && dist[src][i] < minDist) {
minIdx = i;
minDist = dist[src][i];
}
}
if(minIdx < 0) {
break;
}
checkers[minIdx] = 1;
checkCount++;
int nidx = minIdx;
int ndist = minDist;
//src에서 가장 가까운 점 nIdx 를 기점으로 최단경로 재갱신
for (int i = 1; i <= n; i++) {
if (dist[nidx][i] != INF && ndist + dist[nidx][i] < dist[src][i]) {
dist[src][i] = ndist + dist[nidx][i];
}
}
}
return dist[src][dest];
}
위의 소스를 Priority Queue 를 통해 개선한다면 노드의 갯수 N 과 Edge 의 갯수 E 에 대하여 O(E + NlogN) 의 시간 복잡도로 개선할 수 있다.
private static int INF = 1000000000;
private static class Node implements Comparable<Node> {
int idx;
int val;
int getIdx() {
return idx;
}
int getVal() {
return val;
}
Node(int idx, int val) {
this.idx = idx;
this.val = val;
}
@Override
public int compareTo(Node o) {
return this.getVal() - o.getVal();
}
}
/**
* 다익스트라 알고리즘.
* @param dist 최단경로 배열
* @param n 노드의 갯수
* @param src 시작 노드 인덱스
* @param dest 도착 노드 인덱스
* @return
*/
private static int djikstra(int[][] dist, int n, int src, int dest) {
PriorityQueue<Node> priorityQueue = new PriorityQueue<>();
for (int i = 1; i <= n; i++) {
if (src != i && dist[src][i] < INF) {
priorityQueue.offer(new Node(i, dist[src][i]));
}
}
while (!priorityQueue.isEmpty()) {
Node next = priorityQueue.poll();
int nidx = next.getIdx();
int ndist = next.getVal();
for (int i = 1; i <= n; i++) {
if (dist[nidx][i] != INF && ndist + dist[nidx][i] < dist[src][i]) {
dist[src][i] = ndist + dist[nidx][i];
priorityQueue.offer(new Node(i, dist[src][i]));
}
}
}
return dist[src][dest];
}
가장 기본적이면서도 중요한 알고리즘의 하나이고, 여러가지 중요한 아이디어들이 알고리즘에 녹아있기 때문에 잘 알아두고 계속해서 연습해보는 것이 필요하다.
알고리즘은 다음 링크에서 연습해볼 수 있다.
https://www.acmicpc.net/problem/1916
다음읜 위의 문제에 대한 해답 코드이다.
import java.util.PriorityQueue;
import java.util.Scanner;
public class Main {
private static int INF = 1000000000;
private static class Node implements Comparable<Node> {
int idx;
int val;
int getIdx() {
return idx;
}
int getVal() {
return val;
}
Node(int idx, int val) {
this.idx = idx;
this.val = val;
}
@Override
public int compareTo(Node o) {
return this.getVal() - o.getVal();
}
}
private static int djikstra(int[][] dist, int n, int src, int dest) {
PriorityQueue<Node> priorityQueue = new PriorityQueue<>();
for (int i = 1; i <= n; i++) {
if (src != i && dist[src][i] < INF) {
priorityQueue.offer(new Node(i, dist[src][i]));
}
}
while (!priorityQueue.isEmpty()) {
Node next = priorityQueue.poll();
int nidx = next.getIdx();
int ndist = next.getVal();
for (int i = 1; i <= n; i++) {
if (dist[nidx][i] != INF && ndist + dist[nidx][i] < dist[src][i]) {
dist[src][i] = ndist + dist[nidx][i];
priorityQueue.offer(new Node(i, dist[src][i]));
}
}
}
return dist[src][dest];
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
int[][] dist = new int[1001][1001];
for (int i = 0; i < 1001; i++) {
for (int j = 0; j < 1001; j++) {
dist[i][j] = INF;
}
}
for (int i = 0; i < m; i++) {
int a = scanner.nextInt();
int b = scanner.nextInt();
int d = scanner.nextInt();
dist[a][b] = Math.min(dist[a][b], d);
}
int src = scanner.nextInt();
int dest = scanner.nextInt();
System.out.println(djikstra(dist, n, src, dest));
}
}'DataStructure & Algorithm > Algorithm' 카테고리의 다른 글
| 이진탐색트리 확인 알고리즘 (Binary Search Tree Verification Algorithm) (0) | 2019.06.14 |
|---|---|
| LRU Cache Algorithm 정리 (0) | 2019.06.13 |
| 알고리즘 풀이 시 자주 사용되는 bit 연산 모음 (0) | 2019.05.11 |
| 최대공약수(GCD)와 최소공배수(LCM) 를 위한 유클리드 알고리즘 (0) | 2019.05.05 |
| 최소 행렬 곱셈 연산 순서 알고리즘 (Matrix Multiplication) (0) | 2018.12.13 |